원문 URL : http://tutorials.jenkov.com/java-concurrency/amdahls-law.html
!! 쉬운 이해를 위한 의역이 다소 포함되었다.
암달의 법칙은 연산의 병행 처리로 연산 속도를 얼마나 올릴 수 있는지 계산하는 데 쓰일 수 있다. 암달의 법칙은 1967년 이 이론을 발표한 Gene Amdahl 의 이름을 따서 명명되었다. 병행 또는 동시성 시스템으로 작업하는 대부분의 개발자들은 암달의 법칙을 알지 못하더라도 잠재적인 속도 향상에 대한 직관적인 느낌을 가진다. 어쨌든 암달의 법칙은 여전히 알아둘 가치가 있다.
먼저 수학적인 설명 후 다이어그램을 통해 암달의 법칙을 보여주도록 하겠다.
암달의 법칙 정의
병렬화 가능한 프로그램은 두 부분으로 나뉜다.
- 병렬화 불가능한 부분
- 병렬화 가능한 부분
디스크의 파일을 처리하는 프로그램이 있고 가정하자. 프로그램에는 디렉토리를 스캔하여 내부 메모리에 파일의 목록을 생성하는 부분이 있다. 각 파일 정보는 파일을 처리하는 쓰레드로 전달된다. 디렉토리를 스캔하여 파일 목록을 생성하는 부분은 병렬화 불가능한 부분이지만 파일을 처리하는 부분은 병렬화 가능한 부분이다.
순차적으로 실행되는 프로그램의 전체 수행 시간을 T 라고 한다. T 에는 병렬화 가능한 부분과 병렬화 불가능한 부분의 수행 시간이 모두 포함되어 있다. 병렬화 불가능한 부분은 B 라고 한다. 이제 병렬화 가능한 부분은 T - B 라 할 수 있다. 요약하자면 다음과 같다.
- T = 순차적 실행의 전체 수행시간
- B = 병렬화 불가능한 부분 실행의 전체 수행시간
- T - B = 병렬화 가능한 부분의 전체 수행시간 (순차적으로 실행되었을 경우)
그리고 다음과 같이 표현된다.
T = B + (T-B)병렬화 가능한 부분에 대한 부호는 없다는 점에서 위 식은 어딘가 이상해 보이기도 한다. 그러나 식에서 병렬화 가능한 부분은 T 와 B 로 표현될 수 있고, 부호의 수를 줄이면서 식은 개념적으로 축소되었다.
병렬화 가능한 부분을 나타내는 T - B 는 프로그램을 병렬로 실행했을 때 기대할 수 있는 속도 상승 값이다. 속도가 얼마나 향상되는가는 쓰레드나 CPU 를 얼마나 사용하느냐에 달려있다. 쓰레드 또는 CPU 의 수를 N 이라 한다. 병렬화 가능한 부분의 최대 실행 속도는 다음과 같이 계산된다.
(T - B) / N다르게 쓸 수도 있다.
(1/N) * (T - B)위키피디아의 암달의 법칙 문서에는 위 식이 등장한다.
암달의 법칙에 의하면, 프로그램의 병렬화 가능한 부분이 N 개의 쓰레드 혹은 CPU 를 사용하여 실행될 경우 전체 수행시간은 다음과 같이 계산된다.
T(N) = B + (T - B) / NT(N) 은 병렬 처리의 수와 전체 수행시간을 의미한다. 따라서 T 는 T(1) 으로 표현될 수 있다. 병렬 처리 1 에 대한 프로그램 전체 수행시간이다. T(1) 을 사용하면 암달의 법칙은 다음과 같이 표현된다.
T(N) = B + ( T(1) - B ) / N의미는 여전히 같다.
계산 예제
암달의 법칙을 보다 잘 이해하기 위해 계산 예제를 하나 보도록 한다. 프로그램 전체 수행 시간은 1 으로 설정한다. 병렬화 불가능한 부분은 프로그램의 40% 을 자치한다. 수행 시간으로는 0.4 이다. 병렬화 가능한 부분은 1 - 0.4 = 0.6 이 된다.
병렬 처리의 수를 2 라고 하면(2 쓰레드 혹은 CPU) 수행 시간은 다음과 같다.
T(2) = 0.4 + ( 1 - 0.4 ) / 2
= 0.4 + 0.6 / 2
= 0.4 + 0.3
= 0.7같은 식으로 인자를 5 로 바꾸면 다음과 같다.
T(5) = 0.4 + ( 1 - 0.4 ) / 5
= 0.4 + 0.6 / 5
= 0.4 + 0.12
= 0.52그림으로 보는 암달의 법칙
쉬운 이해를 위해 암달의 법칙을 그림으로 설명해본다.
먼저, 프로그램의 병렬화 가능하지 않은 부분을 B 로 두고, 가능한 부분을 1-B 로 둔다.
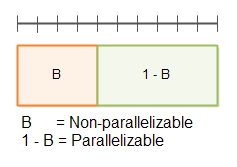
상단의 선은 프로그램 전체 수행시간 T(1) 이다.
병렬 처리의 수가 2 라면 수행 시간을 다음과 같이 표현할 수 있다.
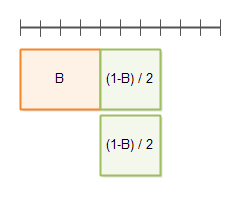
병렬 처리의 수가 3 이라면 다음과 같다.
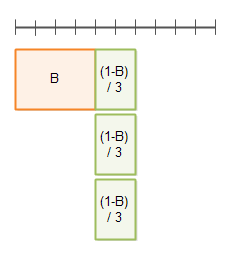
알고리즘 최적화
암달의 법칙에 의하면 병렬화 가능한 부분은 하드웨어에 맡김으로써 더 빠르게 실행될 수 있다. 더 많은 수의 쓰레드/CPU 를 사용하는 것이다. 하지만 병렬화 가능하지 않는 부분의 속도 향상은 코드 최적화를 통해서 이루어질 수 있다. 따라서 병렬화 가능하지 않은 부분의 코드를 최적화 함으로써 프로그램의 속도와 병렬성을 높일 수 있다. 가능하다면 병렬화 가능하지 않는 부분의 처리를 병렬화 가능한 부분으로 옮겨서 병렬화 가능하지 않은 부분을 더 작게 만들 수도 있다.
순차적 수행의 최적화
프로그램에서 순차적으로 수행되는 부분을 최적화한다면, 최적화 후 암달의 법칙을 사용햐ㅐ 프로그램의 실행 시간을 계산해낼 수 있다. 병렬화 가능하지 않은 부분 B 와 병렬 처리의 수 O 으로 계산한다면암달의 법칙은 다음과 같다.
T(O,N) = B / O + (1 - B / O) / N병렬화 가능하지 않은 부분의 실행은 이제 B / O 만큼의 시간을 소모한다. 고로 병렬화 가능한 부분의 실행 시간은 1 - B / O 가 된다.
B 가 0.4 이고 O 가 2, N 은 5 라면 계산은 다음과 같다.
T(2,5) = 0.4 / 2 + (1 - 0.4 / 2) / 5
= 0.2 + (1 - 0.4 / 2) / 5
= 0.2 + (1 - 0.2) / 5
= 0.2 + 0.8 / 5
= 0.2 + 0.16
= 0.36실행 시간 vs 향상된 속도
지금까지는 암달의 법칙을 프로그램의 최적화 또는 병렬화 후 실행 시간을 계산하는 데에 사용해왔다. 암달의 법칙은 향상된 속도, 즉 새로운 알고리즘이나프로그램이 이전 버전보다 얼마나 빨라졌는지를 계산하는 데에도 사용될 수 있다.
올드 버전의 실행 시간을 T 라고 하면, 향상된 속도는 다음과 같다.
Speedup = T / T(O,N)실행 시간이나 향상된 속도를 계산할 때 T 은 주로 1 로 설정한다.
Speedup = 1 / T(O,N)T(O,N) 에 암달의 법칙을 넣으면 식은 다음과 같이 된다.
Speedup = 1 / ( B / O + (1 - B / O) / N )B = 0.4, O = 2, N = 5 라면 계산은 다음과 같이 된다.
Speedup = 1 / ( 0.4 / 2 + (1 - 0.4 / 2) / 5)
= 1 / ( 0.2 + (1 - 0.4 / 2) / 5)
= 1 / ( 0.2 + (1 - 0.2) / 5 )
= 1 / ( 0.2 + 0.8 / 5 )
= 1 / ( 0.2 + 0.16 )
= 1 / 0.36
= 2.77777 ...이 계산이 의미하는 것은, 병렬화 가능하지 않은 부분(순차적 실행)을 인자 2 로 최적화하고 병렬화 가능한 부분을 인자 5 로 병렬화하면 프로그램의 실행은 최대 2.77777 배로 빨라진다는 것이다.
계산에 그치지 말고 측정하라
암달의 법칙을 통해 프로그램의 향상된 속도를 계산해낼 수 있기는 하지만, 이 계산에 지나치게 의존해선 안된다. 실제로 알고리즘을 최적화 또는 병렬화 할 때는 다른 많은 요인들이 작용할 수 있다.
메모리의 속도, CPU 캐시 메모리, 디스크, 네트워크 카드 기타 등등의 것들이 그 제한 요인이 된다. 만약 새 알고리즘이 병렬화 되었으나 CPU 캐시 미스를 더 많이 일으킨다면 CPU 의 수 만큼의 기대했던 속도 향상을 얻을 수 없다. 알고리즘이 메모리 버스나 디스크 혹은 네트워크 카드 또는 커넥션을 지나치게 사용하게 된다면 역시 같은 결과가 발생한다.
암달의 법칙은 프로그램의 어디를 최적화 할 것인지에 대한 아이디어를 얻기 위해 사용하고, 실제로 얼마만큼의 최적화 속도 향상이 있을지는 측정을 통해 알아보아야 한다. 종종 높은 순차적 실행 알고리즘(단일 CPU)은 병렬 알고리즘보다 나은 성능을 보인다. 이유는 간단하다. 순차적 실행은 동시 실행에 따르는 (작업을 중단하고 다시 시작하는 등의)오버헤드가 없고, 단일 CPU 알고리즘은 하드웨어의 작업에 에 더 친화적일 수 있다. (CPU 파이프라인, CPU 캐시 등)
'Java > Concurrency' 카테고리의 다른 글
| 논 블로킹 알고리즘(Non-blocking Algorithms) (2) | 2017.05.27 |
|---|---|
| 동기화 장치 해부(Anatomy of a Synchronizer) (0) | 2017.05.25 |
| 컴페어 스왑(Compare and Swap) (0) | 2017.05.24 |
| 쓰레드 풀(Thread Pools) (0) | 2017.05.22 |
| 블로킹 큐(Blocking Queues) (3) | 2017.05.22 |